archimedes hat-box theorem uniform sphere distribution Let ${\bf u} \in \mathbb{R}^3$ be a random vector with uniform distribution on the three-dimensional unit sphere. Then the projection on any given unit vector $\bf v \in . The answer to your perfectly good question depends on the cubic inches that the Box provides matched against the table of cubic inches required for the number of wires and connectors by wire size in the circuit that you are .
0 · sphere hat box theorem
1 · hat box theorem
2 · archimedes hat box
The lidded tin container is marked with the word "Western Germany" and features a colorful design that is sure to catch the eye. It is perfect for storing cookies, and candies. It a great addition to any collection.
Abstract. Archimedes' hat-box theorem states that uniform measure on a sphere projects to uniform measure on an interval. This fact can be used to derive Simpson's rule. We present .Archimedes’ hat-box theorem states that uniform measure ona sphere projects to uniform measure on an interval. This fact can be used to derive Simpson’s rule. Archimedes' Hat-Box Theorem Enclose a sphere in a cylinder and cut out a spherical segment by slicing twice perpendicularly to the cylinder 's axis. Then the lateral surface area of the spherical segment is equal to the lateral . Let ${\bf u} \in \mathbb{R}^3$ be a random vector with uniform distribution on the three-dimensional unit sphere. Then the projection on any given unit vector $\bf v \in .
Archimedes' Theorem says axial projection of any measurable region on a sphere on the right circular cylinder circumscribed about the sphere preserves area. picture from Archimedes' Hat .
Archimedes' hat-box theorem states that uniform measure on a sphere projects to uniform measure on an interval. This fact can be used to derive Simpson's rule. We present various .Since the unique rotation-invariant distribution on the surface of a sphere of any dimension is the uniform dis-tribution (Theorem 4.1.2 of [6]), the propositions of Archimedes and Herschel .
Archimedes' hat-box theorem states that uniform measure on a sphere projects to uniform measure on an interval. This fact can be used to derive Simpson's rule. We present .U has the uniform distribution on the sphere. That means that if E is any subset of S, then the probability such that U falls into E is proportional to the area A ( E ) of E .
sphere hat box theorem
Theorem (Archimedes) Let f : S2!R be given by (x;y;z) 7!z. Then the pushforward of the standard measure on the sphere to the interval is 2ˇ times Lebesgue measure. arXiv:math/0405366v2 .Abstract. Archimedes' hat-box theorem states that uniform measure on a sphere projects to uniform measure on an interval. This fact can be used to derive Simpson's rule. We present various constructions of, and lower bounds for, numerical cubature formulas using moment maps as a generalization of Archimedes' theorem.Archimedes’ hat-box theorem states that uniform measure ona sphere projects to uniform measure on an interval. This fact can be used to derive Simpson’s rule.
Archimedes' Hat-Box Theorem Enclose a sphere in a cylinder and cut out a spherical segment by slicing twice perpendicularly to the cylinder 's axis. Then the lateral surface area of the spherical segment is equal to the lateral surface area cut out of the cylinder by the same slicing planes, i.e.,
Let ${\bf u} \in \mathbb{R}^3$ be a random vector with uniform distribution on the three-dimensional unit sphere. Then the projection on any given unit vector $\bf v \in \mathbb{R}^3$ $$X = {\bf u}^\mathrm{T} {\bf v}$$ has uniform distribution $$X .
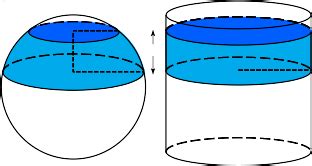
Archimedes' Theorem says axial projection of any measurable region on a sphere on the right circular cylinder circumscribed about the sphere preserves area. picture from Archimedes' Hat-Box Theorem. Enclose a sphere in a cylinder and cut out a spherical segment by slicing perpendicularly to the cylinder's axis.Archimedes' hat-box theorem states that uniform measure on a sphere projects to uniform measure on an interval. This fact can be used to derive Simpson's rule. We present various constructions of, and lower bounds for, numerical cubature formulas using moment maps as a generalization of Archimedes' theorem.Since the unique rotation-invariant distribution on the surface of a sphere of any dimension is the uniform dis-tribution (Theorem 4.1.2 of [6]), the propositions of Archimedes and Herschel-Maxwell suggest the following characterization of mean-zero Gaussian distributions; we provide a proof and discussion of generalizations in the last section. Archimedes' hat-box theorem states that uniform measure on a sphere projects to uniform measure on an interval. This fact can be used to derive Simpson's rule. We present various constructions of, and lower bounds for, numerical cubature formulas using moment maps as a generalization of Archimedes' theorem.
U has the uniform distribution on the sphere. That means that if E is any subset of S, then the probability such that U falls into E is proportional to the area A ( E ) of E .Theorem (Archimedes) Let f : S2!R be given by (x;y;z) 7!z. Then the pushforward of the standard measure on the sphere to the interval is 2ˇ times Lebesgue measure. arXiv:math/0405366v2 [math.NA] 22 Sep 2004 Numerical cubature from ArchimedesÕ hat-box theorem Greg Kuperberg! Department of Mathematics, University of California, Davis, CA 95616Abstract. Archimedes' hat-box theorem states that uniform measure on a sphere projects to uniform measure on an interval. This fact can be used to derive Simpson's rule. We present various constructions of, and lower bounds for, numerical cubature formulas using moment maps as a generalization of Archimedes' theorem.Archimedes’ hat-box theorem states that uniform measure ona sphere projects to uniform measure on an interval. This fact can be used to derive Simpson’s rule.
Archimedes' Hat-Box Theorem Enclose a sphere in a cylinder and cut out a spherical segment by slicing twice perpendicularly to the cylinder 's axis. Then the lateral surface area of the spherical segment is equal to the lateral surface area cut out of the cylinder by the same slicing planes, i.e., Let ${\bf u} \in \mathbb{R}^3$ be a random vector with uniform distribution on the three-dimensional unit sphere. Then the projection on any given unit vector $\bf v \in \mathbb{R}^3$ $$X = {\bf u}^\mathrm{T} {\bf v}$$ has uniform distribution $$X .Archimedes' Theorem says axial projection of any measurable region on a sphere on the right circular cylinder circumscribed about the sphere preserves area. picture from Archimedes' Hat-Box Theorem. Enclose a sphere in a cylinder and cut out a spherical segment by slicing perpendicularly to the cylinder's axis.Archimedes' hat-box theorem states that uniform measure on a sphere projects to uniform measure on an interval. This fact can be used to derive Simpson's rule. We present various constructions of, and lower bounds for, numerical cubature formulas using moment maps as a generalization of Archimedes' theorem.
Since the unique rotation-invariant distribution on the surface of a sphere of any dimension is the uniform dis-tribution (Theorem 4.1.2 of [6]), the propositions of Archimedes and Herschel-Maxwell suggest the following characterization of mean-zero Gaussian distributions; we provide a proof and discussion of generalizations in the last section.
Archimedes' hat-box theorem states that uniform measure on a sphere projects to uniform measure on an interval. This fact can be used to derive Simpson's rule. We present various constructions of, and lower bounds for, numerical cubature formulas using moment maps as a generalization of Archimedes' theorem.
U has the uniform distribution on the sphere. That means that if E is any subset of S, then the probability such that U falls into E is proportional to the area A ( E ) of E .
how to install metal outlet box

how to install metal roof on my house
• The Stainless Steel Laundry Utility Sink with Faucet is the ideal blend of quality, function, and value • This versatile sink is ideal for any kitchen, laundry, mudroom, garage, or food-related business • Easy-to-assemble industrial style metal cabinet with adjustable feetCabinet is pre-assembled; Colour: glossy white; Stainless steel sink and faucet; Soft-close doors; cUPC certified
archimedes hat-box theorem uniform sphere distribution|hat box theorem